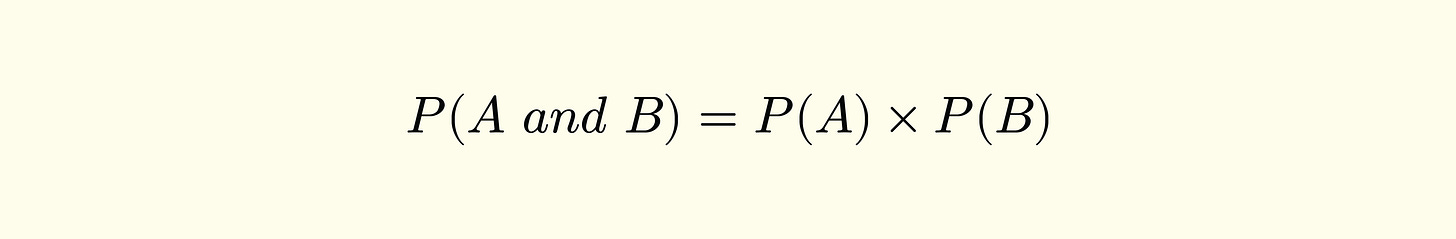Correcting Huberman's Statistics

Probability 101

If you are active on the internet and interested in statistics, then the probability of seeing Andrew Huberman being wrong about statistics is 0.999.

In case you are an outlier, here is the summary:

In his podcast on Fertility Huberman said this:

If you have a 20% chance of pregnancy in any given month, the chance of being pregnant after 6 months is 120%.

That’s clearly wrong. Here is why:

The correct formula to calculate such examples is this:

The formula is the cumulative distribution function (CDF) of a geometric distribution.

But that’s too complicated, so let’s bring it down to grandma’s level.

From the statement above we know for a fact that the probability of pregnancy in a given month is 20%:

If we use the complement rule we can also calculate the probability of not being pregnant.

The complement of an event A is the event that A does not occur. The sum of the probabilities of an event and its complement is always 1.

But that is only for 1 month. In the original example, he mentioned 6 months. Using the multiplication rule for independent events, we can do the math.

Two events are independent if the occurrence of one event does not affect the occurrence of the other.

If events A and B are independent, then:

We have 6 independent events here, so we raise the probability of no pregnancy in a single trial to the power of 6:

If we combine the above we get that:

So, the probability of being pregnant at least once in 6 months is approximately 73.79%.

Now let’s simulate the situation using numpy:

Credit for this code goes to Craig Chirinda:

The output of this code is:

Estimated probability of at least one pregnancy in 6 months: 0.73713 Monthly cumulative probabilities: {1: 0.2, 2: 0.36, 3: 0.49, 4: 0.59, 5: 0.67, 6: 0.74}

The correction

After the reactions online, Huberman released a statement accepting his mistakes.

Please note that during this calculation we don’t consider any biological or other factors. It is purely based on statistics!