Everything about Histograms
The first visual for numerical data
I create a histogram in the first 10 minutes of every analysis. It tells a lot about the data.
By the end of the post, you will understand why I love it. I will explain everything you should know about histograms and how to create them.
What are histograms?
For this post, I will use the Top 650 FIFA 22 Players Dataset from Kaggle, and we will look at the player's height. (Data is in cm).
Simply looking at the values we cannot tell anything. These are just "numbers". Some visuals and statistics will help.
We have 652 data points with a mean of 181.94 and 7.1 standard deviation.
Let's look at the histogram of the same data:
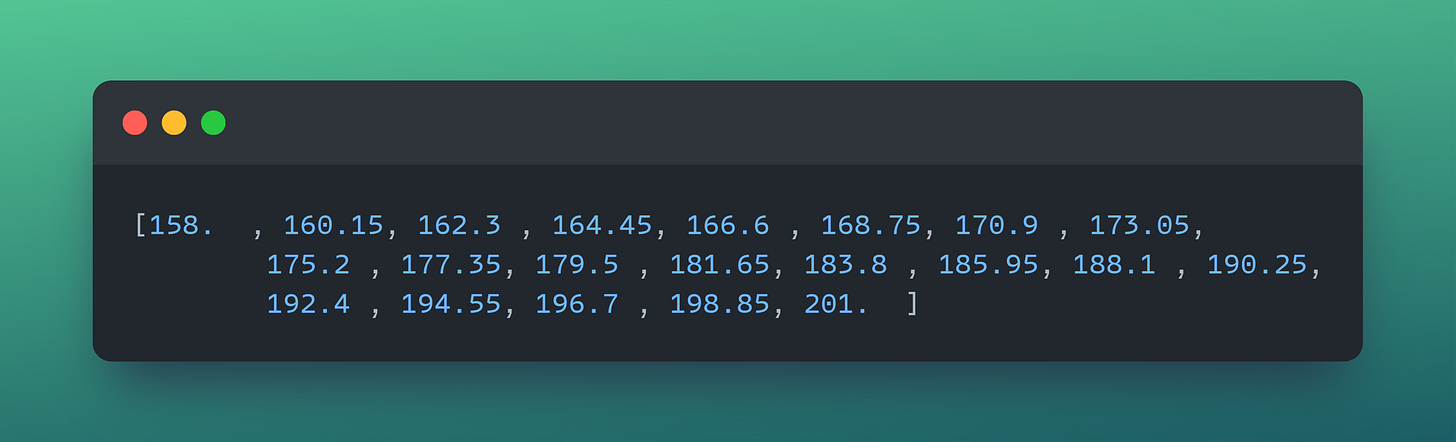
Histograms are good for checking the distribution of the dataset. It shows the frequency of points within a certain range. The ranges are called bins. The bin edges for the chart above are the following:
All but the last (righthand-most) bin is half-open. This means that the first bin is [158, 160.15) (including 158, but excluding 160.15) and the second is [160.15, 162.3). The last bin however includes 201.
Instead of putting the points onto a number line, we created groups (bins) and counted how many points were in one bin. This gives us the height of the bars.
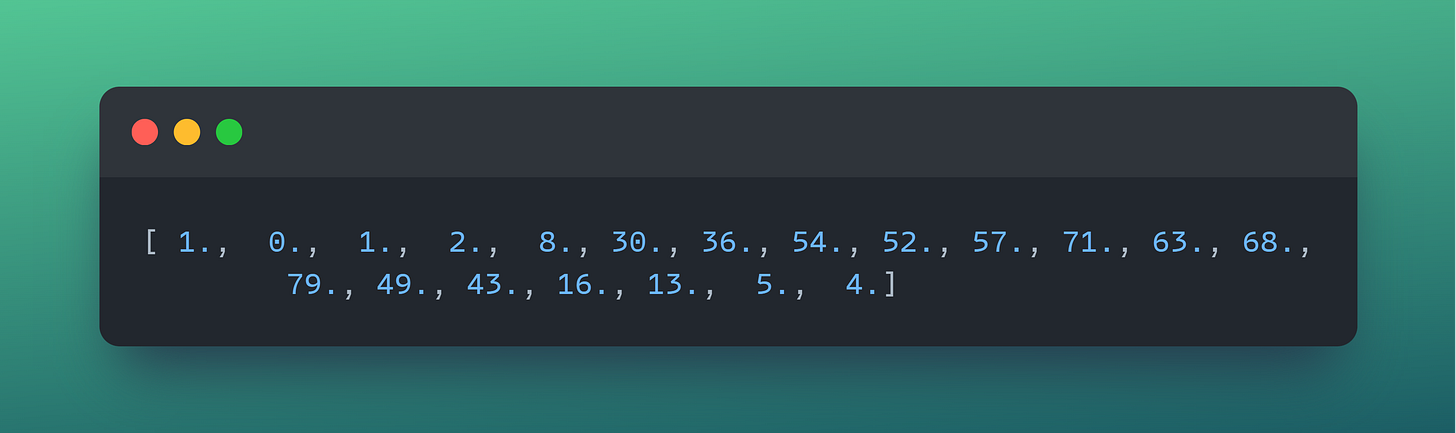
This is how many points are in each bin:
The process of creating histograms
We create the bins:
We can choose a number - in this case, the bins are equal-width. In this example, I used this method with 20 bins.
We can define the bin edges - in this case, the bins may be unequally spaced.
We can use a predefined binning strategy.
(More on these in a later post)
Sort each data point into the appropriate bin.
We are lucky because Python/Matplotlib does the job for us.
In the `plt.hist` I defined the column from the dataset and the number of bins. The rest is just formatting. It's this easy, and we get a lot of info.
What it can show us?
Let's answer the question of why histogram is really useful: Because it can provide so much information. I usually create a histogram in the first 10 minutes of every analysis.
It gives information about the:
Distribution Shape: Whether the data is normally distributed (bell-shaped or not).
Central Tendency: Histograms can give a visual approximation of where the data clusters. In this example, most players are between `[185, 190]` cm. To be specific, 168 of them.
Variability: The spread of the bars indicates the range and variance of the data. A wide spread suggests high variability, while a narrow spread suggests low variability.
Outliers and Gaps: Isolated bars or gaps between bars can indicate outliers or specific clusters in the data. In this case, the player with a height of 158 cm is an outlier.
But consider this:
As you can see in this example, we cannot talk about the right side of the graph as outliers. They are clearly different from the main cluster, but these values (around 100) form their own group.
By the way, this is a bimodal distribution.
Skewness: A Histogram can also show the asymmetry of the distribution. If the tail is longer on the right, the data is right-skewed. If the tail is longer on the left, it's left-skewed.
Kurtosis: By looking at the sharpness of the peaks, we can tell if the data is concentrated around the mean (leptokurtic) or distributed through the whole range of values (platykurtic).
Histograms are not bar graphs
Yes, we use bars to show frequency, but there are clear differences:
Bar graphs:
- The main goal is to compare categories.
- The data is categorical.
- Can have bars reordered to best present the data (e.g., from highest to lowest).
- Have spaces between bars to distinguish between categories.
- Should have bars of equal width since they represent distinct categories and the width is not data-driven.
Histograms:
- Used to understand the distribution of numerical data.
- The data is typically continuous.
- Bars in natural order, since the data is continuous.
- Bars touch each other to show the data is continuous.
- Can have varying bar widths if the bins are unequal
Here is a quick cheat sheet for you:
You can find all the code for this post on this link.